Explorando los tipos de números en matemáticas
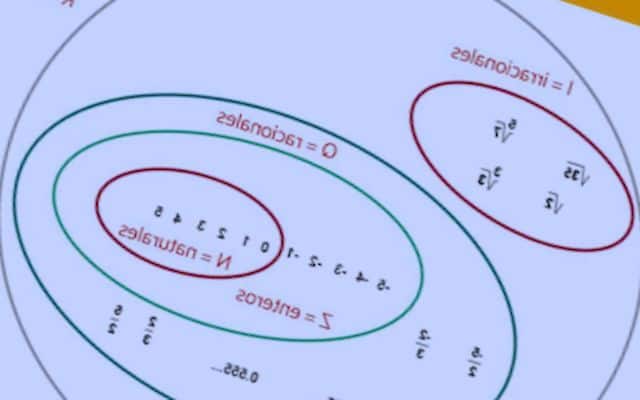
Los números son una parte fundamental de las matemáticas y del mundo que nos rodea. A lo largo de la historia, los humanos hemos desarrollado diversas formas de representar y clasificar los números para poder entender y manejar las distintas situaciones que se nos presentan. En este artículo, exploraremos los diferentes tipos de números que existen en matemáticas y cómo se utilizan en distintos contextos. Desde los números naturales hasta los enteros gaussianos, veremos cómo cada uno de estos números tiene características únicas que los distinguen de los demás.
Números naturales
Los números naturales son aquellos que utilizamos para contar objetos o elementos. Comenzando desde el número 1 y extendiéndose hacia el infinito, los números naturales son una parte esencial de nuestro sistema numérico. Algunos ejemplos de números naturales son 1, 2, 3, 4, 5, y así sucesivamente. Los números naturales también se representan mediante el símbolo "N" en matemáticas.
Números enteros
Los números enteros incluyen todos los números naturales, pero también incluyen sus negativos y el número cero. Los números enteros se representan mediante el símbolo "Z" en matemáticas. Algunos ejemplos de números enteros son -3, -2, -1, 0, 1, 2, 3, y así sucesivamente. Los números enteros son útiles para representar cambios de dirección, temperaturas bajo cero, entre otras cosas.
Números racionales
Los números racionales son aquellos que se pueden expresar como una fracción, es decir, como el cociente de dos números enteros. Los números racionales se representan mediante el símbolo "Q" en matemáticas. Algunos ejemplos de números racionales son 1/2, 3/4, -5/2, 0/1, y así sucesivamente. Sin embargo, no todos los números pueden ser expresados como una fracción, estos números se conocen como irracionales.
Números irracionales
Los números irracionales son aquellos que no se pueden expresar como una fracción simple. Estos números tienen una cantidad infinita de dígitos decimales no repetitivos y no terminales. Algunos ejemplos de números irracionales son π (pi), √2 (raíz cuadrada de 2), y e (la base del logaritmo natural). Estos números son extremadamente importantes en matemáticas y se utilizan en cálculos avanzados y en diversas áreas de la ciencia.
Números decimales
Los números decimales son aquellos que se representan a través de una coma decimal, que separa la parte entera de la parte decimal. Los números decimales son una forma de representar los números racionales en base 10. Algunos ejemplos de números decimales son 0.5, 3.14, -2.75, y así sucesivamente. Los números decimales son utilizados en situaciones que requieren una mayor precisión que los números enteros, como los cálculos financieros o el diseño gráfico.
También te puede interesar:
Números reales
Los números reales incluyen a todos los números racionales e irracionales. Los números reales se representan mediante el símbolo "R" en matemáticas. Los números reales son utilizados en una amplia gama de aplicaciones, desde la física hasta la economía. Los números reales se pueden representar en una línea numérica continua, en la cual los números racionales están espaciados entre sí y los números irracionales están "escondidos" entre ellos.
Números imaginarios
Los números imaginarios son aquellos que se definen como la raíz cuadrada de un número negativo. Los números imaginarios se representan mediante el símbolo "i" en matemáticas. Los números imaginarios son utilizados en cálculos complejos y en ciertas ramas de la física y la ingeniería. Algunos ejemplos de números imaginarios son i, 3i, -2i, y así sucesivamente. Estos números tienen propiedades fascinantes y juegan un papel importante en la solución de ecuaciones cuadráticas.
Números complejos
Los números complejos son aquellos que se pueden expresar como una suma de un número real y un número imaginario. Un número complejo se representa mediante la fórmula "a + bi", donde "a" es la parte real y "b" es la parte imaginaria. Los números complejos son utilizados en diversas áreas de la ciencia y la ingeniería, como en el análisis de circuitos eléctricos y en la teoría de números. Algunos ejemplos de números complejos son 3 + 2i, -1 - 4i, 5i, y así sucesivamente.
Números primos
Los números primos son aquellos que solo son divisibles por 1 y por ellos mismos, es decir, no tienen divisores adicionales. Los números primos son una parte importante de la teoría de números y son utilizados en la criptografía y en la generación de números aleatorios. Algunos ejemplos de números primos son 2, 3, 5, 7, 11, y así sucesivamente. Los números primos tienen propiedades únicas y son objeto de estudio de muchos matemáticos.
Números enteros gaussianos
Los números enteros gaussianos son aquellos que pueden ser expresados como una combinación lineal de un número entero y un número imaginario multiplicado por la unidad imaginaria "i". Los números enteros gaussianos son utilizados en la teoría de números y en la geometría euclidiana. Algunos ejemplos de números enteros gaussianos son 1 + i, -3 + 2i, i, y así sucesivamente.
Conclusión
Los números son una parte fundamental de las matemáticas y de nuestra vida diaria. Desde los números naturales hasta los enteros gaussianos, cada uno de estos números tiene características únicas que los distinguen de los demás. Los números nos permiten contar objetos, realizar cálculos precisos y resolver problemas complejos en diversas áreas de la ciencia y la ingeniería. Es fascinante ver cómo los diferentes tipos de números se entrelazan y se utilizan en conjunto para describir mejor el mundo que nos rodea. A medida que avanzamos en nuestro estudio de las matemáticas, es importante comprender los diferentes tipos de números y cómo se relacionan entre sí.
También te puede interesar:
Deja una respuesta


Relacionado